Hauteurs
Soit ABC un triangle dans lequel la hauteur
issue de C coupe [AB] au point H
AH = 3cm, BH = 6cm et CH = 3cm.
1e ) Calculer BC. En donner
la valeur arrondie au mm près.
(CH) est la hauteur issue de C de ABC, donc BCH est rectangle en H.
BCH est rectangle en H,donc j'applique le théorème de Pythagore.
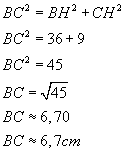
3e )
Quel est l’orthocentre de OAH ? Justifier.
(OH) et (AH) sont deux hauteurs de AOH. L'orthocentre de OAH est donc leur
point d'intersection, H.
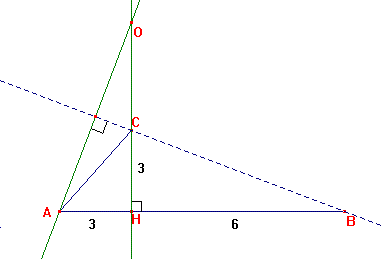
O est le point d'intersection des hauteurs du triangle. On construit par exemple la hauteur issue de A. Elle coupe (CH) au point O.
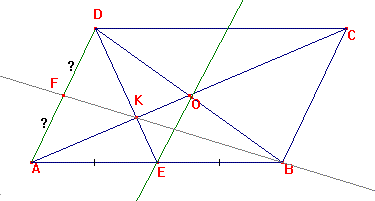
Soit ABCD un parallélogramme de centre O tel
que AB = 8 cm, AD = 6 cm et BD = 7 cm.
La médiane issue de D de ABD coupe
[AB] au point E.
1e ) Montrer que (OE) et (AD) sont parallèles.
(DE) est la médiane issue de D de ABD, donc E est le milieu de [AB].
ABCD est un parallélogramme de centre O, donc O est le milieu de [BD].
Dans
le triangle ABD:
E est le milieu de [AB] et O est le milieu de [BD], donc (OE)//(AD) d'après
le premier théorème des milieux.
2e ) [OA] et [DE] se coupent au point K.
(BK) coupe (AD) au
point F.
Montrer que F est le milieu de [AD].
(DE) et (AO) sont deux médianes de ABD.
Donc K est lecentre de gravité de
ABD.
(BF) passe par le sommet B du triangle ABD et par son centre de gravité,
donc (BF) est la troisième médiane du triangle.
Donc F est le milieu de [AD].
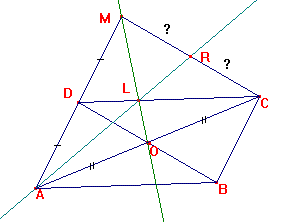
Soit ABCD un parallélogramme
de centre O.
Soit
M le symétrique de A par rapport à D.
(MO) coupe [DC] en L. (AL) coupe
[MC] en R.
Montrer que R est le milieu de [MC].
ABCD est un parallélogramme de centre O, donc O est le milieu de [AC].
Donc (MO) est la médiane issue de M de MAC.
M est le symétrique de A par rapport à D, donc D est le milieu de [AM].
Donc (CD) est la médiane issue de C de MAC.
Donc L est le centre de gravité de MAC.
Donc (AL) est la troisième médiane de MAC, donc R est le milieu de [MC].
Soit ABCD un losange de centre O tel que
AB = 5 cm, BD = 8 cm.
Soit E le symétrique de D par rapport à C.
1e ) Que représente (BC) pour BDE ?
E est le symétrique de D par rapport à C, donc C est le milieu de [DE],
donc (BC) est la médiane isuue de B de BDE.
2e ) Que
représente (OE) pour BDE ?
ABCD est un losange de centre O, donc O est le milieu de [BD], donc (OE)
est la médiane issue de E de BDE.
3e ) (OE) et ( BC ) se coupent
en F. Que représente F pour
BDE ?
F est le point d'intersection des médianes de BDE, donc F est le centre
de gravité de BDE.
4e ) (DF) coupe (BE) au point G. Montrer que G est le milieu
de [BE].
(DF) passe par un sommet de BDE et par son centre de gravité, donc (DF) est
la troisième médiane de BDE. Donc G est le milieu de [BE].
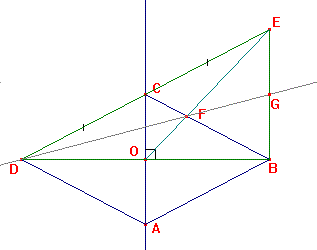
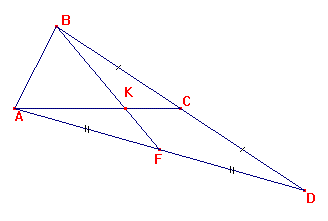
Soit ABC un triangle
tel que AB = 4 cm, BC = 5 cm et CA = 6 cm.
Soit D le symétrique de B par rapport à C.
Soit F le milieu de [AD].
(AC) et (BF) se coupent en K.
a ) Que représente K pour ABD ?
D est le symétrique de B par rapport à C, donc C est le milieu de [BD],
donc (AC) est la médaine issue de A de ABD.
Fest le milieu de [AD], donc (BF) est la médiane issue de B de ABD.
Les deux médianes (BF) et (AC) secoupent en K, donc K est le centre de
gravité de ABD.
b ) Expliquer comment tracer le milieu
H de [AB] en utilisant seulement une règle non graduée.
Pour tracer le milieu de [AB], il faut tracer (DK) qui est la troisièmemédiane
du triangle ABD.