Soit ABCD un carré de 8 cm de côté.
a ) Calculer la mesure de l’angle .
ABCD est un caré donc le triangle ABD est rectangle et isocèle. Donc = 45° .
b ) Calculer au centimètre près la longueur BD.
ABD est rectangle en A, donc j'utilise le théorèmede Pythagore.

(BD) //  (AC).  (AB ) (AC).  BC = BD.
 = 64°. AC = 5 cm.
a ) Montrer que (CD) est la bissectrice de .
BCD est isocèle en B, or dans un triangle isocèle les deux angles à la base sont égaux, donc .
(BD)//(AC), donc les angles sont alternes internes, donc égaux.
Donc , donc (CD) est la bissectrice de .

b ) Calculer   et .
Les deux angles aigus du triangle ABC rectangle en A sont complémentaires, donc =36°.

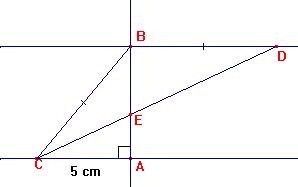
c ) Calculer CE, BC, BD, puis DE . En donner la valeur arrondie au mm.
 = 64°, donc =32°.
Dans ACE rectangle en A,

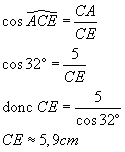
Dans ACB rectangle en A,

c ) Calculer CE, BC, BD, puis DE. En donner la valeur arrondie au mm. (suite)

BD = BC.

(BD) //  (AC) et (AB ) (AC), or si deux droites sot parallèles, alors toute perpendiculaire à l'une est perpendiculaire à l'autre, donc (AB ) (BD).
Dans BED rectangle en B,

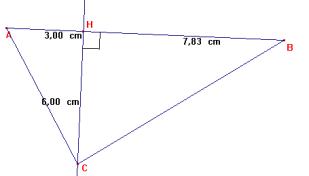
ABC est un triangle rectangle en A. [AH] est sa hauteur issue de A. AC = 3 cm. AH = 2,4 cm.
a ) Indiquer sur la figure les angles de même mesure. Justifier.

b ) Calculer la valeur approchée au degré près de la mesure des angles de la figure. Justifier.

d ) Que peut on calculer  si ABC n’est pas rectangle en A ?
On peut calculer la mesure des angles du triangle rectangle ACH et CH.

c ) Calculer  au millimètre près les longueurs qui manquent.
ACH est rectangle en H, donc j'utilise le théorème de Pythagore.

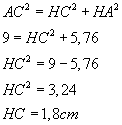
Dans ABC rectangle en A,

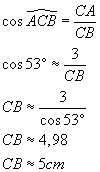
Dans ABH rectangle en H,

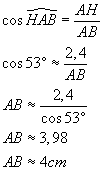
Soit ABCD un parallélogramme tel que : 
 mesure 52°, [ AD ] mesure 5 cm,  ( AD ) et 
(BD) sont perpendiculaires.
1^e  ) a ) Quelle est la mesure de  ? Justifier.
ABCD est un parallélogramme, or les angles opposés d'un parallélogramme sont égaux, donc =52°.
        b ) Quelle est la mesure de  ? Justifier.
Deux angles consécutifs d'un parallélogramme sont supplémentaires ( leur somme est 180°), donc
=180°-52°
=128°
2^e  ) Calculer AB. En donner la valeur approchée au millième près.
Dans ABD rectangle en D,

3^e  ) La perpendiculaire à (CD) passant par A coupe (CD) en H.
a ) Montrer que la mesure de  est 52°. Justifier.
ABCD est un parallélogramme, donc (AB)//(CD).
et sont alternes interne, donc égaux. Donc = 52°

3^e ) b ) Calculer DH. En donner la valeur approchée au dixième près.

Dans ADH rectangle en H,

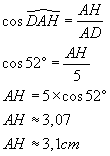
Construire un parallélogramme ABCD tel que AB = 7 cm, mesure 52° et   mesure 38°.
1^e ) a ) Calculer la mesure de l’angle . Que peut on en déduire pour le triangle ABC ?
La somme de mesures des angles d'un triangle est 180°.
=180°-(52°+38°)
=90°
b ) Calculer la valeur approchée de BC au millimètre près.
Dans ABC rectangle en C

c ) Quelle est la mesure de l’angle ? Justifier.
ABCD est un parallélogramme, donc (AB)// (CD).
et sont alternes internes, donc égaux. Donc =38°.

2^e ) Soit F le symétrique de B par rapport à C.
a ) Construire le parallélogramme DCFE.

b )  Quelle est la mesure de l’angle ? Justifier.
(AB)//(CD)
et sont correspondants, donc égaux. Donc =52°.
c)  Quelle est la mesure de l’angle ? Justifier.
CDEF est un parallélogramme. Or dans un parallélogramme deux angles consécutifs sont suppléméntaires. Donc
et sont supplémentaires.
= 180°-52°
= 128°.

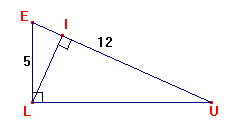
Construire un triangle ELU rectangle en L tel que
EL = 5 cm et  EU  = 12 cm.
1^e ) Calculer la valeur approchée au degré près de la mesure de l’angle .
Dans LEU rectangle en L

2^e ) Montrer que la valeur approchée au degré près de la mesure de l’angle est 25°.
Les deux angles aigus d'un triangle rectangle sont complémentaires, donc 90°-65°
25°
3^e ) Calculer la valeur approchée de LU au millimètre près.
ELU est un triangle rectangle, donc j'utilise le théorème de Pythagore.

4^e ) Soit (LI) la hauteur issue de L du triangle LEU.

a) Calculer la valeur arrondie au degré de la mesure de l’angle .
Les deux angles aigus d'un triangle rectangle sont complémentaires, donc 25°.
b ) Calculer la valeur approchée au millimètre près de LI.
(IL) est la hauteur isue de L de ELU, donc ELI est rectangle en I.
Dans le triangle ELI rectangle en I

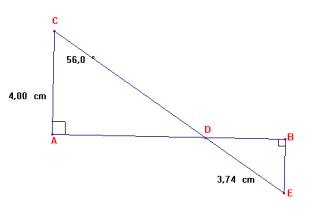
ABC est un triangle rectangle en B tel que AB = 10 cm et AC = 11 cm.
1^e  ) Calculer la valeur arrondie au degré près de la mesure de l'angle .
2^e  ) En déduire la valeur arrondie au degré près de  est 65°.
3^e  ) Calculer BC. En donner  la valeur arrondie au mm .
4^e  ) Le cercle de diamètre [AB] coupe (AC) au point K.
a ) Que peut on dire du triangle ABK ?
b ) Calculer la valeur arrondie au millimètre de AK