Parallèles et perpendiculaires

Construire deux droites parallèles d1 et d2.
Construire une droite d, perpendiculaire à d1.
Que peut on dire de d et d2 ?
d1//d2 et dd1, or si deux droites sont parallèles, alors toute perpendiculaire à l'une est perpendiculaire à l'autre, donc dd2.

 Construire une droite d.
Construire deux droites d1 et d2, perpendiculaires à d.
Que peut on dire de d1 et d2 ?
d1d et d2d, or si deux droites sont perpendiculaires à la même droite, alors ces deux droites sont parallèles, donc d1//d2.

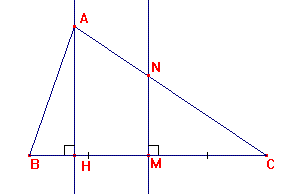
Construire un triangle ABC.
Construire la droite (AH), hauteur de ABC.
Construire la médiatrice de [BC]. Elle coupe [BC] en M et [CA] en N .
Que peut on dire de (AH) et (MN ) ? le démontrer.
(AH) hauteur de ABC, donc (AH) (BC).
(MN) médiatrice de [BC], donc (MN) (BC).
(AH) (BC) et (MN) (BC), or si deux droites sont perpendiculaires à la même droite, alors ces deux droites sont parallèles, donc (AH)//(MN).

TIC et TAC sont deux triangles. Montrer que les hauteurs issues de I et de A sont parallèles.
Soit (AH) la hauteur issue de A de TAC. (AH)(TC).
Soit (IK) la hauteur issue de I de TIC. (IK) (TC).
(AH)(TC) et (IK) (TC) or si deux droites sont perpendiculaires à la même droite, alors ces deux droites sont parallèles, donc (AH)//(KI).

Deux segments  [AB ] et [CD ] ont la même médiatrice. Que peut-on dire de ( AB ) et ( CD ) ?
d est la médiatrice de [AB], donc d (AB).
d est la médiatrice de [CD], donc d (CD).
d (AB) et d (CD), or si deux droites sont perpendiculaires à la même droite, alors ces deux droites sont parallèles, donc (AB)//(CD).

Soit [AB] un segment tel que AB = 3cm. Soit C  le cercle de centre A qui passe par B.
Soit t la tangente en B au cercle  C .
1e  ) Que peut on dire de t et (AB) ? Justifier.
t tangente en B au cercle  C de rayon [AB], donc
t (AB).
2e  ) La parallèle à t qui passe par A coupe le cercle C en  E et F.
Que peut on dire de  (EF) et (AB) ? Le démontrer.
t//(EF) et t (AB), or si deux droites sont parallèles, alors toute perpendiculaire à l'une est perpendiculaire à l'autre, donc (EF) (AB).
3e  ) Que représente (AB) pour [EF] ? Le démontrer.
(EF) est un diamètre du cercle C, donc A est le milieu de [EF].
De plus (EF) (AB), donc (AB) est la médiatrice de (EF).