Théorème des milieux : parallèles
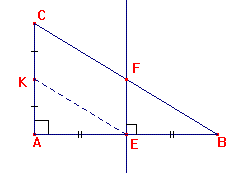
Soit ABC un triangle rectangle en A. La médiatrice de [BA] coupe [AB] au point E et [BC] au point F. Soit K le milieu de [AC]. 1^e ) Démontrer que (EF) et (AC) sont parallèles. ABC est un triangle rectangle en A, donc (AC)(AB) (EF) est la médiatrice de [AB], donc (EF)(AB). (AC)(AB) et (EF)(AB), or si deux droites sont perpendiculaires à la même droite, alors ces deux droites sont parallèles, donc (EF)//(AC). 2^e ) Démontrer que (BC) et (KE ) sont parallèles. (EF) est la médiatrice de [AB], donc E est le milieu de [AB]. K est le milieu de [AC]. Or la droite qui passe par les milieux de deux côtés d'un triangle est parallèle au troisième côté, donc (BC)//(KE).
Théorème des milieux : longueurs
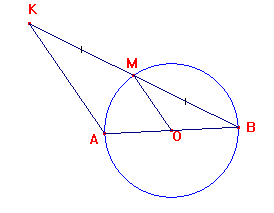
Soit C un cercle de centre O et de rayon 4 cm. Soit [AB] un diamètre de ce cercle. Soit M un point de C tel que BM = 6 cm. Soit K le symétrique de B par rapport à M. a ) Quelle est la mesure de [OM ] ? Justifier. M est un point du cercle de centre O et de rayon 4 cm, donc OM = 4 cm. b ) Calculer le périmètre du triangle ABK. K est le symétrique de B par rapport à M donc M est le milieu de [BK], donc BK = 12 cm. [AB] est un diamètre du cercle, donc O est le milieu de [AB]. Dans le triangle ABK, M est le milieu de [BK] et O est le milieu de [AB], or le segment qui joint les milieux de deux côtés d'un triangle mesure la moitié du troisième côté, donc AK = 2OM, AK = 8 cm. AB + BK + KA = 8 + 12 +8 AB + BK + KA = 28 Le périmètre de ABK est 28 cm.
Théorème des milieux : milieu
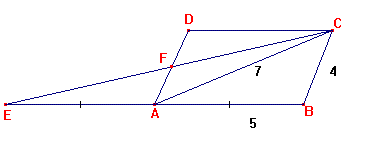
Soit ABCD un parallélogramme tel que AB = 5 cm, BC = 4 cm et AC = 7 cm. Soit E le symétrique de B par rapport à A. (EC) coupe (AD ) au point F. Montrer que F est le milieu de [EC]. E est le symétrique de B par rapport à A, donc A est le milieu de [EB]. ABCD est un parallélogramme, donc(AD)//(BC). Dans le triangle BAC, A est le milieu de [EB] et (AD)//(BC), or la droite qui passe par le milieu d'un côté du triangle et qui est parallèle au deuxième côté coupe le troisième côté en son milieu, donc F est le milieu de [EC].
ABCD est un parallélogramme. La médiatrice de [AB] coupe (AB) en E, (CD) en F et (AC) en K. 1^e ) Que peut on dire de (CD) et (EF ) ? ABCD est un parallélogramme, donc (AB)// ( CD). (EF) est la médiatrice de [AB], donc (EF)(AB). (AB)// ( CD) et (EF)(AB), or Si deux droites sont parallèles, alors toute perpendiculaire à l'une est perpendiculaire à l'autre, donc (EF) (CD). 2^e ) La perpendiculaire à (CD) passant par B coupe (CD) en H  et (AC) en I. Que représente K pour [AI] ? (EF) (CD) et (BH) (CD), or si deux droites sont perpendiculaires à la même droite, alors ces deux droites sont parallèles, donc (BH)//(FE). (EF) est la médiatrice de [AB], donc E est le milieu de [AB]. Dans le triangle ABI, E est le milieu de [AB] et (EF)//(BH), or la droite qui passe par le milieu d'un côté du triangle et qui est parallèle au deuxième côté coupe le troisième côté en son milieu, donc K est le milieu de [AI].