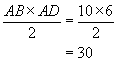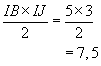Mélange
Premier théorème des milieux : la droite qui passe par les milieux de deux côtés d'un triangle est parallèle au troisième côté. Deuxième théorème des milieux : le segment qui joint les milieux de deux côtés d'un triangle mesure la moitié du troisième côté. Troisième théorème des milieux : la droite qui passe par le milieu d'un côté d'un triangle et qui est parallèle au deuxième côté coupe le troisième côté en son milieu.
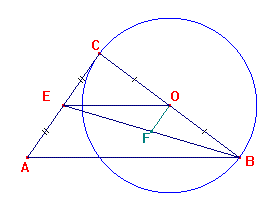
Soit ABC un triangle tel que AB = 8cm, BC = 6 cm et AC = 5 cm. Soit C le cercle de diamètre [BC]. Soit O son centre. La médiane issue de B du triangle ABC coupe (AC) au point E. 1^e ) Que peut on dire de (OE) et ( AB ) ? Le démontrer. O est le centre du cercle de diamètre [BC], donc O est le milieu de [BC]. (BE) est la médiane de ABC, donc E est le milieu de [AC]. O est le milieu de [BC] et E est le milieu de [AC], donc (OE)//(AB) d'après le premier théorème des milieux. 2^e ) Soit F le milieu de [BE]. Calculer OF. Justifier. AC = 5 cm, et E est le milieu de [AC], donc EC = 2,5 cm Dans le triangle BEC, O est le milieu de [BC] et F est le milieu de [EB], donc 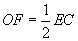d'après le deuxième théorème des milieux. Donc EF = 1,25 cm.
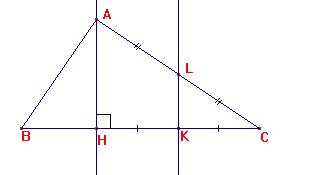
ABC est un triangle quelconque. Soit [AH] la hauteur issue de A de ABC. Soit K le milieu de [CH] et L le milieu de [AC]. Montrer que (KL) est la médiatrice de [CH]. Dans le triangle ACH, K est le milieu de [CH] et L est le milieu de [AC], donc (KL)//(AH) d'après le premier théorème des milieux. (AH) hauteur de ABC, donc (AH) (BC) (KL)//(AH) et (AH) (BC), or si deux droites sont parallèles, alors toute perpendiculaire à l'une est perpendiculaireà l'autre, donc (KL) (CH). K est le milieu de [CH] et (KL) (CH), donc (KL) est la médiatrice de [CH].
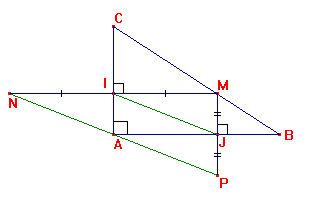
ABC est un triangle rectangle en A tel que AB = 6 cm et AC = 4 cm. Soit M le point de [BC] tel que BM = 2 cm. Soit N le symétrique de M par rapport à (AC). (MN) et (AC) se coupent au point I. Soit P le symétrique de M par rapport à (AB). (MN) et (AB) se coupent au point J. 1^e ) Que peut on dire de JAIM ? Le démontrer. ABC est un triangle rectangle en A donc (AB) (AC). N est le symétrique de M par rapport à (AC), donc (MN) (AC). P est le symétrique de M par rapport à (AB), donc (MP) (AB). JAIM a trois angles droits, donc JAIM est un rectangle par définition. 2^e ) Montrer que (IJ)//(NP). N est le symétrique de M par rapport à (AC), donc I est le milieu de [MN]. P est le symétrique de M par rapport à (AB), donc J est le milieu de [MP]. I est le milieu de [MN] et J est le milieu de [MP], donc (IJ)//(MP) d'après le premier théorème des milieux.
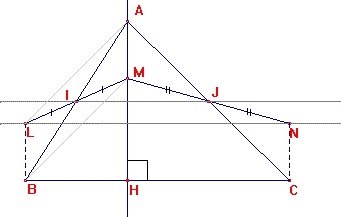
Soit ABC un triangle tel que AB = 10 cm, BC = 12 cm et AC = 14 cm. Soient I et J les milieux respectifs de [ AB ] et [ AC ]. La hauteur issue de A de ABC coupe [ BC ] en H. Soit M le point de [ AH ) tel que AM = 3 cm. Soit N le symétrique de M par rapport à J. Soit L le symétrique de M par rapport à I. 1 ) Que peut on dire de ( IJ ) et ( BC ) ? Le démontrer. Calculer IJ. Dans ABC, I est le milieu de [AB] et J est le milieu de [AC], donc (IJ)//(BC) d'après le premier théorème des milieux. Dans le triangle ABC, I est le milieu de [AB] et J est le milieu de [AC], donc IJ =1/2 BC d'après le premier théorème des milieux. 2 ) a ) Que peut on dire de ( IJ ) et ( LN ) ? Le démontrer. L est le symétrique de M par rapport à I donc I est le milieu de [ML]. N est le symétrique de M par rapport à J donc J est le milieu de [MN]. Dans le triangle MLN, I est le milieu de [ML] et J est le milieu de [MN], donc (IJ)//(LN) d'après le premier théorème des milieux. b ) Calculer LN Dans le triangle MLN, I est le milieu de [ML] et J est le milieu de [MN], donc IJ =1/2 LN d'après le deuxième théorème des milieux. D'après la première question IJ = 1/2 BC, donc IJ = BC IJ = 12 cm. 3 ) Montrer que CBLN est un parallélogramme. (IJ)//(BC) et (IJ)//(LN) donc (BC)//(LN). De plus IJ = BC, or si un quadrilatère a deux côtés parallèles et égaux, alors ce quadrilatère est un parallélogramme, donc CBLN est un parallélogramme.
	4 ) Que peut on dire de ALBM ? Le démontrer. I est le milieu de [AB] et de [ML], or si un quadrilatère a des diagonales qui se coupent en leur milieu, alors ce quadrilatère est un parallélogramme, donc ALBM est un parallélogramme. 5 ) Que peut on dire de (LB ) et ( CB ) ? Le démontrer. ALBM est un parallélogramme, donc (LB)//(AM), donc (LB)//(AH). (AH) est la hauteur issue de A de ABC, donc (AH)(BC). (LB)//(AH) et (AH(BC) or si deux droites sont parallèles, alors toute perpendiculaire à l'une est perpendiculaire à l'autre, donc (LB)(BC). 6 ) Que peut on dire de CBLN ? Le démontrer. CBLN est un parallélogramme et (LB)(BC), or si un parallélogramme a un angle droit, alors ce parallélogramme est un rectangle, donc CBLN est un rectangle.
1^e ) Construire un triangle ACD isocèle et rectangle en C, tel que AC = 8 cm. Soit J le milieu de [ AC ]. La parallèle à ( CD ) passant par J coupe [ AD ] en K. Montrer que K est le milieu de [ AD ]. Dans ACD, J est le milieu de [AC] et (JK)//(CD), donc K est le milieu de [AD] d'après le troisième théorème des milieux. 2^e ) Montrer que ( JC ) et ( JK ) sont perpendiculaires. ACD est rectangle en C, donc (CD) (AC). (CD) (AC) et (JK)//(CD), or si deux droites sont parallèles, alors toute perpendiculaire à l'une est perpendiculaire à l'autre, donc (JK) (AC), donc (JK) (JC). 3^e ) La perpendiculaire à (CD) passant par K coupe (CD) au point H. Montrer que JKCH est un rectangle. (CD) (AC) et (JK) (JC) et (CH) (HK), or un quadrilatère qui a trois angles droits est un rectangle, donc JKCH est un rectangle. 4^e ) Montrer que H est le milieu de [ CD ]. JKHC est un rectangle, donc (CA)//(HK). (CA)//(HK) et K milieu de [AD], donc H est le milieu de [CD] d'après le troisième théorème des milieux.
	5^e ) Montrer que JC = CH. ACD est isocèle en C, donc CA = CD. J est le milieu de [AC] et H est le milieu de [CD], donc CJ = CH. 6^e ) En déduire la nature du quadrilatère CJKH. JKCH est un rectangle dont deux côtés consécutifs sont égaux, donc JKCH est un carré.
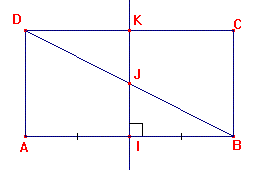
ABCD est un rectangle tel que AB = 10 cm et AD = 6 cm. La médiatrice de [AB] coupe (AB) en I, (BD) en J et (CD) en K. 1^e ) Montrer que J est le milieu de [BD]. (IJ) est la médiatrice de [AB], donc (IJ) (AB). ABCD est un rectangle, donc (AD) (AB). (IJ) (AB) et (AD) (AB) or si deux droites sont perpendiculaires à la même droite, alors ces deux droites sont parallèles, donc (IJ)//(AD). (IJ) est la médiatrice de [AB], donc I est le milieu de [AB]. Dans le triangle ABD, I est le milieu de [AB] et (IJ)//(AD), donc J est le milieu de [BD] d'après le troisième théorème des milieux. 2^e ) Calculer IJ. Justifier. Dans le triangle ABD, I est le milieu de [AB] et (IJ)//(AD), donc IJ = 1/2 AD d'après le deuxième théorème des milieux. Donc IJ = 3 cm.
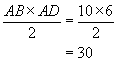
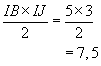
	3^e ) a ) Comparer l’aire de BIJ et l’aire de BAD. Aire de BAD: Aire de BIJ: L'aire de BIJ est égale au quart de l'aire de BAD. b ) Comparer l’aire de BIJ et celle de ABCD L'aire de ABCD est le double de l'aire de BAD, donc l'aire de BIJ est égale au huitième de l'aire du rectangle ABCD.
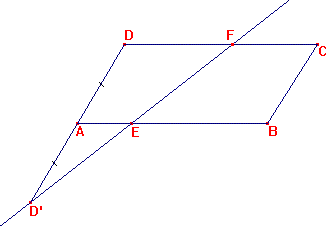
Tracer un parallélogramme ABCD et D’ le symétrique de D par rapport à A. Soit E un point de [AB] et F le point d’intersection des droites (D’E) et (DC). 1^e ) Montrer que E est le milieu de [D’F]. D' est le symétrique de D par rapport à A, donc A est le milieu de [DD']. ABCD est un parallélogramme, donc (AE)//(DC). Dans DD'F, A est le milieu de [DD'] et (AE)//(DF), donc E est le milieu de [D'F] d'après le troisième théorème des milieux. 2^e ) Que peut on dire des longueurs AE et DF ? justifier . Dans le triangle DD'F, A est le milieu de [DD'] et E est le milieu de [D'F], donc AE = 1/2 DF d'après le deuxième théorème des milieux. 3^e ) Où doit être situé E sur [AB] pour que F soit situé en C ? Justifier. DF = DC, donc AE = 1/2 DC, donc E est le milieu de [AB]. Si E est le milieu de [AB], alors F et C sont confondus.
On sait que AD = DE = EB, et que CG = GF = FB. 1^e ) Montrer que (EF) et (GD) sont parallèles. Dans le triangle BDG, F est le milieu de [BG] et E est le milieu de [BD], donc (EF)//(DG) d'après le premier théorème des milieux. 2^e ) Montrer que K est le milieu de [AF]. Dans le triangle AEF, D est le milieu de [AE] et (DK)//( EF), donc K est le milieu de [AF] d'après le troisième théorème des milieux. 3^e ) Comparer DK et DG. D est le milieu de [AE] et K est le milieu de [AF], donc KD = 1/2 EF d'après le deuxième théorème des milieux. Dans le triangle BDG, E est le milieu de [BD] et F est le milieu de [BG], donc EF= 1/2 DG d'après le deuxième théorème des milieux. Donc KD = 1/4 DG. 4^e ) Montrer que (DG) et (AC) sont parallèles. Dans le triangle AFC, G est le milieu de [FC] et K est le milieu de [AF], donc (KG)//(AC), donc (GD)//(AC).
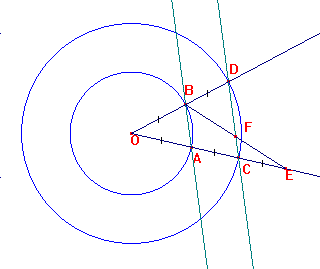
Deux cercles de centre O ont pour rayon R et 2R. 1^e ) Montrer que (AB) et (CD ) sont parallèles. OC = 2 OA, et O, A et C sont alignés, donc A est le milieu de [OC]. OD = 2OB et O, B et C sont alignés, donc B est le milieu de [OD]. Dans le triangle OCD, A est le milieu de [OC] et B est le milieu de [OD], donc (AB)//(CD) d'après le premier théorème des milieux. 2^e ) Soit E le symétrique de A par rapport à C. (BE) et (CD) se coupent en F. Que représente F pour [BE] ? le démontrer. E est le symétrique de A par rapport à C, donc C est le milieu de [AE]. Dans le triangle ABE, C est le milieu de [AE] et (FC) // (AB), donc F est le milieu de [BE] d'après le troisième théorème des milieux.