Démonstration des deux premiers théorèmes des milieux
	On sait que : M est le milieu de [AB] N est le milieu de [AC] On construit le point K tel que N soit le milieu de [MK] On veut prouver que (MN) et (BC) sont parallèles, et que BC = 2MN.
	1^e ) Que peut on dire de AKCM ? Le démontrer. N est le milieu de [AC] et N est le milieu de [MK], or si un quadrilatère a des diagonales qui se coupent en leur milieu, alors ce quadrilatère est un parallélogramme, donc AKCM est un parallélogramme.
	2^e ) Que peut on en déduire pour a ) (AM) et (CK ) ? AKCM est un parallélogramme, donc (AM)//(CK). b) AM et CK ? AKCM est un parallélogramme, or si un quadrilatère est un parallélogramme, alors ses côtés opposés sont égaux, donc AM=CK.
	3^e ) Que peut on en déduire pour BM et CK ? M est le milieu de [AB], donc BM = AM. AM = CK, donc BM = CK.
	4^e ) Que peut on en déduire pour BCKM ? BM=CK et (BM)//(CK), or si un quadrilatère a deux côtés à la fois parallèles et égaux, alors ce quadrilatère est un parallélogramme, donc BKCM est un parallélogramme.
	5^e ) Que peut on en déduire pour a ) (MN) et (BC) ? BKCM est un parallélogramme, donc (MN)//(BC). b ) MN et BC ? BKCM est un parallélogramme, or si un quadrilatère est un parallélogramme, alors ses côtés opposés sont égaux, donc MK = BC. N est le milieu de [MK], donc MN = 1/2MK. Donc MN = 1/2BC.
Synthèse  : Si dans un triangle ABC M est le milieu de [AB] et N est le milieu de [AC), alors : (MN)//(BC) et MN = 1/2 BC.
Théorèmes des milieux
I. Soit ABC un triangle. Soit I le milieu de [AB]. Soit J le milieu de [AC]. 1^e ) a ) Que peut on dire de IJ et BC ? Le démontrer. I est le milieu de [AB] et J est le milieu de [AC], donc IJ = 1/2 BC, d'après le deuxième théorème des milieux b ) Que peut on dire de (IJ) et (BC) ? Le démontrer. I est le milieu de [AB] et J est le milieu de [AC], donc (IJ)//(BC), d'après le premier théorème des milieux. 2^e ) Soit M un point intérieur au triangle AIJ. Soit K le symétrique de M par rapport à I . Soit L le symétrique de M par rapport à J. Que peut on dire de (IJ) et ( KL) ? de IJ et KL ? Le démontrer. K est le symétrique de M par rapport à I, donc I est le milieu de [KM]. L le symétrique de M par rapport à J, donc J est le milieu de [ML]. I est le milieu de [KM] et J est le milieu de [ML], donc (IJ)//(KL) d'après le premier théorème des milieux et IJ = 1/2 KL d'après le deuxième théorème des milieux. 4^e ) Que peut on dire de (KL) et (BC ) ? (IJ)//(BC) et (IJ)//KL), donc (KL)//(BC). De KL et BC ? Le démontrer. IJ = 1/2 KL et IJ = 1/2 BC, donc KL = BC.
	5^e ) Que peut on dire de KLCB ? Le démontrer. (KL)//(BC) et KL = BC, or si un quadrilatère a deux côtés à la fois parallèles et égaux, alors ce quadrilatère est un parallélogramme, dnc KLCB est un paralélogramme. 6^e ) Où doit on placer le point M pour que KLCB soit un rectangle ? Si M appartient à la perpendiculaire à (BC) passant par A, alors KLBC est un rectangle.
II. Soit ABCD un rectangle de centre O tel que AB = 10 cm ; AD = 6 cm. Soit E le milieu de [AD ]. Soit F le milieu de [ AB ]. 1. Que peut on dire de ( EF ) et ( BD ) ? de EF et BD ? Le démontrer. Dans le triangle ABD, E est le milieu de [AD]et F est le milieu de [ AB ], donc (EF)//(BD) d'après le premier théorème des milieux et EF = BD d'après le deuxième théorème des milieux. 2. Que peut-on dire de ( EO ) et ( AB ) ? Le démontrer. Calculer EO. ABCD est un rectangle, or les diagonales d'un rectangle se coupent en leur milieu, donc O est le milieu de [BD]. Dans le triangle ABD, O est le milieu de [BD] et E est le milieu de [AD], donc (OE)//(AB) d'après le premier théorème des milieux et OE = 1/2 AB d'après le deuxième théorème des milieux. Donc OE = 5cm.
	3. Que peut on dire de EOBF ? Le démontrer. F est le milieu de [AB], donc FB = 5 cm. Donc OE = FB. (OE)/(AB) et OE = AB, or si un quadrilatère a deux côtés à la fois parallèles et égaux, alors ce quadrilatère est un parallélogramme, donc EOBF est un parallélogramme. 4. Que peut on dire de EOFA ? Le démontrer. EOFA est un parallélogramme ( démonstration analogue à celle de la question 3. ) ABCD est un rectangle, donc (EA)(AF). EOFA est un paralélogramme qui a un angle droit, donc EOFa est un rectangle.
III. C et C’ deux cercles de centres O et O’ qui se coupent en A et B. (OA ) coupe C en M, ( O’A) coupe C’ en M’. Que peut on dire de ( OO’ ) et (MM’ ) ? Le démontrer. [AM] est un diamètre du cercle C de centre O, donc O est le milieu de [AM]. [AM'] est un diamètre du cercle C' de centre O', donc O' est le milieu de [AM']. Dans le triangle AMM', O est le milieu de [AM] et O' est le milieu de [AM'], donc (OO')//(MM') d'après le premier théorème des milieux.
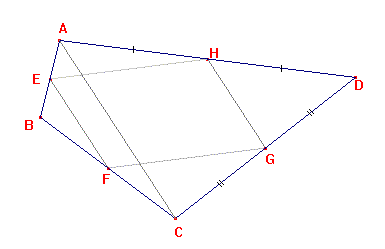
IV. théorème de Warignon. Soit ABCD un quadrilatère quelconque. Soient E,F,G et H les milieux respectifs de [AB], [BC],[CD] et [DA].Que peut on dire de EFGH ? Le démontrer. Je trace la diagonale [AC]. Dans le triangle ABC, E est le milieu de [AB] et F es le milieu de [BC], donc (EF) // (AC) d'après le premier théorème des milieux et EF = 1/2 AC d'après le deuxième théorème des milieux. Dans le tiangle ACD, on démontre de façon analogue que HG =1/2 AC et (HG) // ( AC). (EF) // (AC) et (HG) // ( AC), donc (EF)//(HG). EF = 1/2 AC et HG =1/2 AC, donc EF = HG. (EF)//(HG) et EF = HG, or un si un quadrilatère a deux côtés à la fois parallèles et égaux, alors ce quadrilatère est un parallélogramme donc EFGH est un paraléloramme.