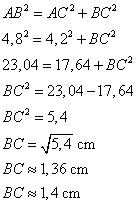Théorème de Pythagore : applications directes
Indiquer les triangles dans lesquels on peut utiliser le théorème de Pythagore, puis l’écrire, et calculer la longueur manquante. En donner la valeur exacte et la valeur arrondie au millimètre. Penser à vérifier que l'hypoténuse est plus longue que les autres côtés!
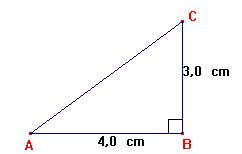ABC est rectangle en B, donc j'utilise le théorème de Pythagore.	On ne peut pas calculer la longueur du troisième côté d'un triangle quelconque. Elle peut varier ici entre 0,8 cm ( 4,9 - 4,1) et 9 cm ( 4,9 + 4,1).
ABC est rectangle en B, donc j'utilise le théorème de Pythagore.	C appartient au cercle de diamètre [AB], donc ABC est rectangle en C. AB = 4,8 cm ABCest rectangle en C,donc j'utilise le théorème de Pythagore.
Le triangle ABC n'est pas un triangle rectangle. On ne peut pas calculer AB.
	ACH est un triangle rectangle rectangle en H, donc j'utilise le théorème de Pythagore.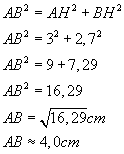	ABH est un triangle rectangle en H, donc j'utilise le théorème de Pythagore.
(DE)//(AC) et (AC)(BC), or si deux droites sont parallèles, alors toute perpendiculaire à l'une est perpendiculaire à l'autre, donc (AC)(BC). BED est rectangle en D, donc j'utilise le théorème de Pythagore.	Le triangle BAC est rectangle en C, mais on ne connaît aucune mesure. On ne peut rien calculer.