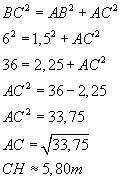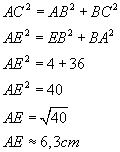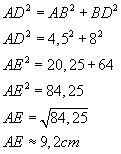Théorème de Pythagore
Une échelle de 6 m est posée contre un cerisier. Le pied de l’échelle est à 1,5 m du tronc de l’arbre. Un homme de 1,80 m, dont la main peut s’élever de 50 cm plus haut que le sommet de sa tête, peut-il atteindre les dernières cerises situées à 8 m du sol ? Justifier la réponse. On suppose que l'arbre est vertical et le sol horizontal. Le triangle ABC est rectangle en A, donc j'utlilise le théorème de Pythagore. 5,80 + 1,80 + 0,50 = 8,10 Si cet homme téméraire peut aller jusqu'en haut de l'échelle, il atteindra la hauteur de 8,10 m. En principe, il atteint les cerises.
1^e ) Soit ABC un triangle rectangle en B tel que AC = 10 cm et BC = 8 cm. Montrer que AB = 6 cm. ABC est un triangle rectangle en B, donc j'utilise le théorème de Pythagore. 2^e ) Placer le point E sur [CB) tel que E Ï [BC] et EB = 2 cm. Calculer AE. En donner la valeur arrondie au millimètre près. EBA est un triangle rectangle en B, donc j'utilise le théorème de Pythagore.
	3^e ) Que peut on dire du triangle ACE ? Pourquoi ? EC = AB +BC EC =10 cm, donc le triangle ACE est isocèle en E.
1^e ) Soit ABCD un parallélogramme tel que AB = 4,5 cm BD = 8 cm et (AB) ^ (BD) Calculer AD. En donner la valeur arrondie au millimètre près. ABD est un triangle rectangle en B, donc j'utilise le théorème de Pythagore. 2^e ) Montrer que le périmètre de ABCD mesure moins de 30 cm. ABCD est un parallélogramme, or les côtés opposés d'un parallélogramme sont égaux, donc AD = BC et AB = CD. en arrondissant par excès. Le périmètre de ABCD mesure moins de 30 cm. 3^e ) Soit O le point d’intersection des diagonales de ABCD et K le milieu de [BC]. Calculer OK.
Soit ABCD un losange dont les diagonales se coupent au point O, tel que AB = 8 cm, AC = 6 cm. 1^e ) Calculer OA. ABCD est un losange, or les diagonales d'un losange se coupent en leur milieu, donc OA = 3 cm. 2^e ) Que peut on dire du triangle OAB ? ABCD est un losange,or les diagonales d'un losange sont perpendiculaires, donc AOB est rectangle en O. 3^e ) a ) Calculer BO. AOB est rectangle en O, donc j'utilise le théorème de Pythagore. b ) En déduire BD. En donner la valeur approchée au millimètre près.	Calcul de la deuxième diagonale du losange.
Soit C un cercle de centre O et de rayon 5 cm. Soit [AB] un diamètre de ce cercle. Soit M un point du cercle tel que AM = 4 cm 1^e ) Montrer que le triangle ABM est un triangle rectangle. M est un point du cercle de diamètre [AB], donc ABM est rectangle en M. 2^e ) La parallèle à ( AM ) passant par O coupe [BM] en E. Montrer que OEB est un triangle rectangle en E. (OE)//(AM) et (AM)(MB), or si deux droites sont parallèles, alors toute perpendiculaire à l'une est perpendiculaire à l'autre, donc (OE)(MB). Donc OMB est un triangle rectangle en E. 3^e ) Montrer que OE = 2 cm. (OE)//(AM), donc j'utilise le théorème de Thalès dans le triangle ABM. 4^e ) Calculer EB. En donner la valeur approchée au millimètre près. OEB est un triangle rectangle en E, donc j'utilise le théorème de Pythagore.
Soit ABC un triangle de hauteur (AH) tel que AH = 3cm , BH = 4 cm et AC = 4 cm. 1^e ) Calculer AB. ABC est un triangle rectangle en B, donc j'utilise le théorème de Pythagore. 2^e ) Calculer CH. En donner la valeur approchée au millimètre près.
Soit C un cercle de centre O et de rayon 4 cm. Soient [AB] et [CD] deux diamètres perpendiculaires de ce cercle. 1^e ) Montrer que ACBD est un carré. Les diagonales de ABCD se coupent en leur milieu, donc ABCD est un parallélogramme. De plus elles sont égales, donc ABCD est un rectangle. De plus elles sont perpendiculaires, donc ABCD est un losange. Donc ABCD est un rectangle et un losange, c'est à dire un carré. 2^e ) Calculer AC. AOC est un triangle rectangle en O, donc j'utilise le théorème de Pythagore.	Calcul de la longueur du côté d'un carré connaissant la diagonale.