Soit ABCD un carré de 8 cm de côté.

a ) Calculer la mesure de l’angle .

b ) Calculer au centimètre près la longueur BD.

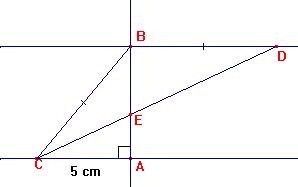
(BD) //  (AC).  (AB ) (AC).  BC = BD.

 = 64°. AC = 5 cm.

a ) Montrer que (CD) est la bissectrice de .

b ) Calculer   et .

c ) Calculer CE, BC, BD, puis DE. En donner la valeur arrondie au mm.

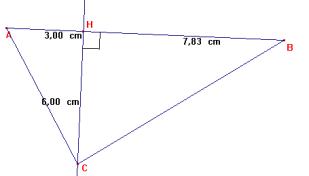
ABC est un triangle rectangle en A. [AH] est sa hauteur issue de A. AC = 3 cm. AH = 2,4 cm.

a ) Indiquer sur la figure les angles de même mesure. Justifier.

b ) Calculer la valeur approchée au degré près de la mesure des angles de la figure. Justifier.

c ) Calculer  au millimètre près les longueurs qui manquent.

d ) Que peut on calculer  si ABC n’est pas rectangle en A ?

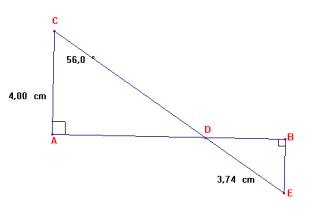
Soit ABCD un parallélogramme tel que :   mesure 52°, [ AD ] mesure 5 cm,  ( AD ) et 

(BD) sont perpendiculaires.

1^e  ) a ) Quelle est la mesure de  ? Justifier.

       b ) Quelle est la mesure de  ? Justifier.

2^e  ) Calculer AB. En donner la valeur approchée au millième près.

3^e  )3^e  ) La perpendiculaire à (CD) passant par A coupe (CD) en H.

a ) Montrer que la mesure de  est 52°. Justifier.

b ) Calculer DH. En donner la valeur approchée au dixième près.

Construire un parallélogramme ABCD tel que AB = 7 cm, mesure 52° et   mesure 38°.

1^e ) a ) Calculer la mesure de l’angle . Que peut on en déduire pour le triangle ABC ?

b ) Calculer la valeur approchée de BC au millimètre près.

c ) Quelle est la mesure de l’angle ? Justifier.

2^e ) Soit F le symétrique de B par rapport à C.

a ) Construire le parallélogramme DCFE.

b )  Quelle est la mesure de l’angle ? Justifier.

c)  Quelle est la mesure de l’angle ? Justifier.

Construire un triangle ELU rectangle en L tel que EL = 5 cm et  EU  = 12 cm.

1^e ) Calculer la valeur approchée au degré près de la mesure de l’angle .

2^e ) Montrer que la valeur approchée au degré près de la mesure de l’angle est 25°.

3^e ) Calculer la valeur approchée de LU au millimètre près.

4^e ) Soit (LI) la hauteur issue de L du triangle LEU.

a) Calculer la valeur arrondie au degré de la mesure de l’angle .

b ) Calculer la valeur approchée au millimètre près de LI.

ABC est un triangle rectangle en B tel que AB = 10 cm et AC = 11 cm.

1^e  ) Calculer la valeur arrondie au degré près de la mesure de l'angle .

2^e  ) En déduire la valeur arrondie au degré près de  est 65°.

3^e  ) Calculer BC. En donner  la valeur arrondie au mm .

4^e  ) Le cercle de diamètre [AB] coupe (AC) au point K.

a ) Que peut on dire du triangle ABK ?

b ) Calculer la valeur arrondie au millimètre de AK