Vocabulaire de base de la géométrie
Pour la mise à jour, des compléments et tous les autres niveaux du collège :
Mate tes Maths
Droite
![]()
(AB)
illimitée
une droite n'a pas de longueur!
Demi
droite
![]()
[AB)
limitée par A, mais pas par B.
Segment
![]()
[AB]
limité par A et par B.
un segment a une longueur
Distance
AB
AB est la longueur du segment [AB].
On peut écrire, par exemple,
AB = 8 cm.
Milieu d'un segment

Le
milieu d'un segment est le point du segment situé à égale
distance des extrémités.
Pour prouver qu'un point est le milieu
d'un segment, il faut donc prouver deux longueurs égales, mais
aussi que les points sont alignés!
Médiatrice
d'un segment

La médiatrice d'un segment est la perpendiculaire à ce segment en son milieu.
Condition pour qu'un point appartienne à la médiatrice d'un segment
Si
un point est à égale distance des deux extrémités
d'un segment, alors c'est un point de la médiatrice du segment.
C'est
cette propriété que l'on utilise pour construire la médiatrice
d'un segment avec un compas.
Propriété
des points de la médiatrice d'un segment

Tout
point de la médiatrice d'un segment est à égale distance
des deux extrémités du segment.
image mobile.

Si
deux droites sont perpendiculaires à la même droite, alors
ces deux droites sont parallèles entre elles.


ABC est un triangle rectangle en A.
[BC] est l'hypoténuse du triangle: c'est le côté opposé à l'angle droit, et le côté le plus long du triangle.

AB = AC, donc ABC est un triangle isocèle en A.
Les deux angles à la base d'un triangle isocèle sont égaux.

AB = BC = CA, donc ABC est un triangle équilatéral.
Dans un triangle équilatéral, les trois angles sont égaux et mesurent chacun 60°.
Hauteur

Une hauteur dans un triangle est une droite aui passe par un sommet et qui est perpendiculaire au côté opposé.
Sur l'image mobile, on peut constater en faisant bouger les sommets du triangle que la hauteur peut être à l'extérieur du triangle.
Médiane

Une
médiane dans un triangle est une droite qui passe par un sommet
et par le milieu du côté opposé.
image mobile

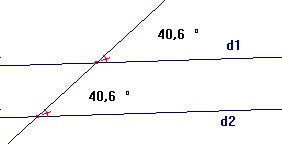
d1 et d2 sont parallèles.
Les deux angles sont alternes internes.
Deux angles alternes internes sont égaux.
image mobile
d1 et d2 sont parallèles.
Les deux angles sont correpondants
Deux angles correspondants sont égaux.
image mobile

Définition:
Un parallélogramme est un quadrilatère dont les côtés
sont parallèles deux à deux.
Propriétes
du parallélogramme:
- dans un parallélogramme, les côtés opposés
sont égaux
- dans un parallélogramme, les diagonales se coupent en leur milieu
- dans un parallélogramme, le point d'intersection des diagonales
est le centre de symétrie. On l'appelle le centre du parallélogramme
- dans un parallélogramme, les angle opposés sont égaux,
et les angles consécutifs sont supplémentaires.
image mobile
Conditions pour qu'un quadrilatère soit un parallélogramme
- si un quadrilatère a des côtés opposés égaux deux à deux, alors c'est un parallélogramme.
- si un quadrilatère à deux côtés à la fois parallèles et égaux, alors c'est un parallélogramme.
- si un quadrilatère a un centre de symétrie, alors c'est un parallélogramme.
- si un quadilatère a des diagonales qui se coupent en leur milieu, alors c'est un parallélogramme.
Rectangle

Un rectangle est un quadrilatère qui a trois angles droits ( donc il en a quatre).
Propriétés:
Un rectangle est un parallélogramme.
Donc il a toutes les propriétés du parallélogramme.
- les diagonales d'un rectangle sont égales.
- un rectangle a deux axes de symétrie
: les médiatrices des côtés.
image mobile
Conditions pour qu'un parallélogramme soit un rectangle
-
si
un parallélogramme a des diagonales égales, alors c'est
un rectangle.
- si un parallélogramme a un angle droit, alors c'est un rectangle.
Losange

Un losange est un quadrilatère qui a quatre côtés égaux.
Propriétés:
Un losange est un parallélogramme.
Donc il a toutes les propriétés du parallélogramme.
de plus:
- les diagonales d'un losange sont perpendiculaires.
- un losange a deux axes de symétrie
: les diagonales.
image mobile
Conditions pour qu'un parallélogramme soit un losange
-
si un parallélogramme a des diagonales perpendiculaires, alors
c'est un losange.
- si un parallélogramme a deux côtés consécutifs
égaux, alors c'est un losange.
Carré

Un carré est un rectangle et un losange.
Un
carré a donc toutes les propriétés du parallélogramme,
du rectangle et du losange.
image mobile
Conditions pour qu'un parallélogramme soit un carré
Toutes les combinaisons sont possibles. Il faut prouver que le quadrilatère est un losange et aussi un rectangle.
![]() exercices(constructions
et descriptions)
exercices(constructions
et descriptions)
exercices(angles droits)
